
For immediate release: Scientists at the Min Planck Institute announced today that placing a pickle on your nose can improve telekinetic ability.
According to the researchers, they performed a study in which a volunteer was asked to place a pickle on her nose and then flip a coin to see whether or not the pickle would help her flip heads. The volunteer flipped the coin, which came up heads.
“This is a crowning achievement for our research,” the study’s authors said. “Our results show that having a pickle on your nose allows you to determine the outcome of a coin-toss.”
Let’s say you’re browsing the Internet one day, and you come across this report. Now, you’d probably think that there was something hinkey about this experiment, right? We know intuitively that the odds of a coin toss coming up heads are about 50/50, so if someone puts a pickle on her nose and flips a coin, that doesn’t actually prove a damn thing. But we might not know exactly how that applies to studies that don’t involve flipping coins.
So let’s talk about our friend p. This is p.
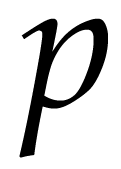
p represents the probability that a scientific study’s results are total bunk. Formally, it’s the probability that results like the ones observed could occur even if the null hypothesis is true. In English, that basically means that it represents how likely it is to get these results even if whatever the study is trying to show doesn’t actually exist at all, and so the study’s results don’t mean a damn thing.
Every experiment (or at least every experiment seeking to show a relationship between things) has a p value. In the nose-pickle experiment, the p value is 0.5, which means there is a 50% chance that the subject would flip heads even if there’s no connection between the pickle on her nose and the results of the experiment.
 There’s a p value associated with any experiment. For example if someone wanted to show that watching Richard Simmons on television caused birth defects, he might take two groups of pregnant ring-tailed lemurs and put them in front of two different TV sets, one of them showing Richard Simmons reruns and one of them showing reruns of Law & Order, to see if any of the lemurs had pups that were missing legs or had eyes in unlikely places or something.
There’s a p value associated with any experiment. For example if someone wanted to show that watching Richard Simmons on television caused birth defects, he might take two groups of pregnant ring-tailed lemurs and put them in front of two different TV sets, one of them showing Richard Simmons reruns and one of them showing reruns of Law & Order, to see if any of the lemurs had pups that were missing legs or had eyes in unlikely places or something.
But here’s the thing. There’s always a chance that a lemur pup will be born with a birth defect. It happens randomly.
So if one of the lemurs watching Richard Simmons had a pup with two tails, and the other group of lemurs had normal pups, that wouldn’t necessarily mean that watching Mr. Simmons caused birth defects. The p value of this experiment is related to the probability that one out of however many lemurs you have will randomly have a pup with a birth defect. As the number of lemurs gets bigger, the probability of one of them having a weird pup gets bigger. The experiment needs to account for that, and the researchers who interpret the results need to factor that into the analysis.
If you want to be able to evaluate whether or not some study that supposedly shows something or other is rubbish, you need to think about p. Most of the time, p is expressed as a “less than or equal to” thing, as in “This study’s p value is <= 0.005″. That means “We don’t know exactly what the p value is, but we know it can’t be greater than one half of one percent.”
A p value of 0.005 is pretty good; it means there’s a 0.5% chance that the study is rubbish. Obviously, the larger the p value, the more skeptical you should be of a study. A p value of 0.5, like with our pickle experiment, shows that the experiment is pretty much worthless.
There are a lot of ways to make an experiment’s p value smaller. With the pickle experiment, we could simply do more than one trial. As the number of coin tosses goes up, the odds of a particular result go down. If our subject flips a coin twice, the odds of getting a heads twice in a row are 1 in 4, which gives us a p value of 0.25–still high enough that any reasonable person would call rubbish on a positive trial. More coin tosses still give successively smaller p values; the p value of our simple experiment is given (roughly) by 1/2n, where n is the number of times we flip the coin.
There’s more than just the p value to consider when evaluating a scientific study, of course. The study still needs to be properly constructed and controlled. Proper control groups are important for eliminating confirmation bias, which is a very powerful tendency for human beings to see what they expect to see and to remember evidence that supports their preconceptions while forgetting evidence which does not. And, naturally, the methodology has to be carefully implemented too. A lot goes into making a good experiment.
And even if the experiment is good, there’s more to deciding whether or not its conclusions are valid than looking at its p value. Most experiments are considered pretty good if they have a p value of .005, which means there’s a 1 in 200 chance that the results could be attributed to pure random chance.
That sounds like it’s a fairly good certainty, but consider this: That’s about the same as the odds of flipping heads on a coin 8 times in a row.

Now, if you were to flip a coin eight times, you’d probably be surprised if it landed on heads every single time.
But, if you were to flip a coin eight thousand times, it would be surprising if you didn’t get eight heads in a row somewhere in there.
One of the hallmarks of science is replicability. If something is true, it should be true no matter how many people run the experiment. Whenever an experiment is done, it’s never taken as gospel until other people also do it. (Well, to be fair, it’s never taken as gospel period; any scientific observation is only as good as the next data.)
So that means that experiments get repeated a lot. And when you do something a lot, sometimes, statistical anomalies come in. If you flip a coin enough times, you’re going to get eight heads in a row, sooner or later. If you do an experiment enough times, you’re going to get weird results, sooner or later.
So a low p value doesn’t necessarily mean that the results of an experiment are valid. In order to figure out if they’re valid or not, you need to replicate the experiment, and you need to look at ALL the results of ALL the trials. And if you see something weird, you need to be able to answer the question “Is this weird because something weird is actually going on, or is this weird because if you toss a coin enough times you’ll sometimes see weird runs?”
That’s where something called Bayesian analysis comes in handy.
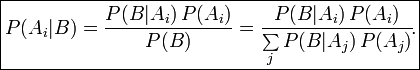
I’m not going to get too much into it, because Bayesian analysis could easily make a post (or a book) of its own. In this context, the purpose of Bayesian analysis is to ask the question “Given the probability of something, and given how many times I’ve seen it, could what I’m seeing can be put down to random chance without actually meaning squat?”
For example, if you flip a coin 50 times and you get a mix of 30 heads and 20 tails, Bayesian analysis can answer the question “Is this just a random statistical fluke, or is this coin weighted?”
When you evaluate a scientific study or a clinical trial, you can’t just take a single experiment in isolation, look at its p value, and decide that the results must be true. You also have to look at other similar experiments, examine their results, and see whether or not what you’re looking at is just a random artifact.
I ran into a real-world example of how this can fuck you up a bit ago, where someone on a forum I belong to posted a link to an experiment that purports to show that feeding genetically modified corn to mice will cause health problems in their offspring. The results were (and still are) all over the Internet; fear of genetically modified food is quite rampant among some folks, especially on the political left.
The experiment had a p value of <= .005, meaning that if the null hypothesis is true (that is, there is no link between genetically modified corn and the health of mice), we could expect to see this result about one time in 200.
So it sounds like the result is pretty trustworthy…until you consider that literally thousands of similar experiments have been done, and they have shown no connection between genetically modified corn and ill health in test mice.
If an experiment’s p value is .005, and you do the experiment a thousand times, it’s not unexpected that you’d get 5 or 6 “positive” results even if the null hypothesis is true. This is part of the reason that replicability is important to science–no matter how low your p value may be, the results of a single experiment can never be conclusive.
A p value of 0.005 is pretty good; it means there’s a 0.5% chance that the study isn’t rubbish.
I think you meant to write that there is an 0.5% chance that the study is rubbish—but that’s not what a p value measures. A p values measures Pr(result at least this extreme | null hypothesis (H0) true), whereas I believe by “the chance the study is rubbish” you mean the false discovery rate (FDR), Pr(H0 true | this result). Of course, Bayes’ Theorem can get you the FDR (or, more accurately, the q value) from the p value, but to invoke it you need the prior probability that H0 is true, which may be difficult to obtain in an objective manner. In certain circumstances, Pr(H0) may be estimated fairly accurately, as in genetic linkage analysis in which one causal gene in the genome is assumed, or empirically, as in a genomewide genetic association study with tests at 1,000,000 markers, nearly all of which are truly not associated with the trait under study.
Yep, you’re right…fixed now.
I’m using somewhat informal language, but by “the study is rubbish” what I mean is that these results could have been obtained even if the null hypothesis is true–in which case, you can’t rely on the results to convince yourself that the null hypothesis is not true. 🙂
Ah, yes; that’s a big problem in genetics, too, since all sorts of confounding can cause false positive results with minuscule p values.
I’m actually thinking about writing a similar essay about confounding factors, now that you mention it. (I keep tossing around the idea of doing a podcast called The Skeptical Pervert, in which I use sex to explain basic scientific literacy and critical thinking skills, but I haven’t had the time to get it rolling yet. I’ve scripted out the first episode, which is a discussion of confounding factors in cause/effect relationships, but I haven’t managed to find the time to sit down and start recording.)
A p value of 0.005 is pretty good; it means there’s a 0.5% chance that the study isn’t rubbish.
I think you meant to write that there is an 0.5% chance that the study is rubbish—but that’s not what a p value measures. A p values measures Pr(result at least this extreme | null hypothesis (H0) true), whereas I believe by “the chance the study is rubbish” you mean the false discovery rate (FDR), Pr(H0 true | this result). Of course, Bayes’ Theorem can get you the FDR (or, more accurately, the q value) from the p value, but to invoke it you need the prior probability that H0 is true, which may be difficult to obtain in an objective manner. In certain circumstances, Pr(H0) may be estimated fairly accurately, as in genetic linkage analysis in which one causal gene in the genome is assumed, or empirically, as in a genomewide genetic association study with tests at 1,000,000 markers, nearly all of which are truly not associated with the trait under study.
Yep, you’re right…fixed now.
I’m using somewhat informal language, but by “the study is rubbish” what I mean is that these results could have been obtained even if the null hypothesis is true–in which case, you can’t rely on the results to convince yourself that the null hypothesis is not true. 🙂
Ah, yes; that’s a big problem in genetics, too, since all sorts of confounding can cause false positive results with minuscule p values.
Re: Yup!
I actually had no idea who Kass was when I picked up the book, but I picked it up as a counter to all the other bioethics stuff I was reading at the time since it definitely is slanted in the “potential problems with human cloning” direction. Mainly why I would suggest it is because I would imagine most readers of your blog are at least of slight trans-humanist bent, myself included, an Kass is helpful in understanding the implications, potential problems, and general resistance to genetic modification. Plus, it’s a diminutive book – and Wilson seems to have balanced out a lot of Kass radicalism seen in his independent publications.
Re: Yup!
Are you familiar with James Hughes at all? He wrote the book Citizen Cyborg, and founded the Institute for Ethics and Emerging Technologies.
I think he does a very good job at talking about the potential problems of new biotechnologies, especially nanotechnology and radical longevity, without being reactionary or Liddite like Kass is. In Citizen Cyborg, he particularly talks about the dangers of creating a classist society in which only certain people have access to emerging biotech at the expense of other people, which is (I think) a lot more compelling an argument in favor of moderation of developing biotechnology than Kass’ religious arguments are. (Hughes was a member of the World Transhumanist Society until a lot of folks in it, who tend to be very Libertarian in their sensibilities, became quite angry about Citizen Cyborg and interpreted it as an attack on the ethics of no-holds-barred, winner-takes-all Extropianism.)
Re: Yup!
I actually had no idea who Kass was when I picked up the book, but I picked it up as a counter to all the other bioethics stuff I was reading at the time since it definitely is slanted in the “potential problems with human cloning” direction. Mainly why I would suggest it is because I would imagine most readers of your blog are at least of slight trans-humanist bent, myself included, an Kass is helpful in understanding the implications, potential problems, and general resistance to genetic modification. Plus, it’s a diminutive book – and Wilson seems to have balanced out a lot of Kass radicalism seen in his independent publications.
By all that’s improbable, this.
Thankyou.
Truly, thankyou.
Good straight forward explanations of probability are hard to come by, especially applied probability that you can tie to a field. Don’t get me started on stochastic methods in simulation, or the horrors of psuedo-random number generators.
If you put this and a dozen or so other pieces of your wisdom in an ebook I’d buy it. If it was on a print-on-demand service I’d not only buy a few copies as gifts I’d recommend a couple of academics I know recommend it to their students.
Re: By all that’s improbable, this.
Thanks! 🙂
By all that’s improbable, this.
Thankyou.
Truly, thankyou.
Good straight forward explanations of probability are hard to come by, especially applied probability that you can tie to a field. Don’t get me started on stochastic methods in simulation, or the horrors of psuedo-random number generators.
If you put this and a dozen or so other pieces of your wisdom in an ebook I’d buy it. If it was on a print-on-demand service I’d not only buy a few copies as gifts I’d recommend a couple of academics I know recommend it to their students.
One of the few occasions I regret LJ’s lack of the [Like] button.
One of the few occasions I regret LJ’s lack of the [Like] button.
Re: Yup!
Are you familiar with James Hughes at all? He wrote the book Citizen Cyborg, and founded the Institute for Ethics and Emerging Technologies.
I think he does a very good job at talking about the potential problems of new biotechnologies, especially nanotechnology and radical longevity, without being reactionary or Liddite like Kass is. In Citizen Cyborg, he particularly talks about the dangers of creating a classist society in which only certain people have access to emerging biotech at the expense of other people, which is (I think) a lot more compelling an argument in favor of moderation of developing biotechnology than Kass’ religious arguments are. (Hughes was a member of the World Transhumanist Society until a lot of folks in it, who tend to be very Libertarian in their sensibilities, became quite angry about Citizen Cyborg and interpreted it as an attack on the ethics of no-holds-barred, winner-takes-all Extropianism.)
I’m actually thinking about writing a similar essay about confounding factors, now that you mention it. (I keep tossing around the idea of doing a podcast called The Skeptical Pervert, in which I use sex to explain basic scientific literacy and critical thinking skills, but I haven’t had the time to get it rolling yet. I’ve scripted out the first episode, which is a discussion of confounding factors in cause/effect relationships, but I haven’t managed to find the time to sit down and start recording.)
Re: By all that’s improbable, this.
Thanks! 🙂
Actually, the easiest way evaluate a scientific study, is whether or not the findings are published in a reputable academic journal. Scientists love new discoveries and have no reason to oppress legit findings. Journalists and others who are looking to attract readers have a bad habit of completely misinterpreting scientific studies, including publishing supposed scientific studies which are anything but scientific.
exactly where you get the idea that flipping a coin 8,000 times it would be surprising if you didn’t get 8 heads or tails in a row is beyond me. It simply isn’t true
the rest of your article sounds as if it were logical, unfortunately there is much more to statistical analyzing the data collected from a real scientific experiment. What you have listed in this post more closely aligns with the “experiments” web publications such as Sciencedaily reports on, and there is a reason those experiments are not published in reputable scientific journals
Actually, the easiest way evaluate a scientific study, is whether or not the findings are published in a reputable academic journal. Scientists love new discoveries and have no reason to oppress legit findings. Journalists and others who are looking to attract readers have a bad habit of completely misinterpreting scientific studies, including publishing supposed scientific studies which are anything but scientific.
exactly where you get the idea that flipping a coin 8,000 times it would be surprising if you didn’t get 8 heads or tails in a row is beyond me. It simply isn’t true
the rest of your article sounds as if it were logical, unfortunately there is much more to statistical analyzing the data collected from a real scientific experiment. What you have listed in this post more closely aligns with the “experiments” web publications such as Sciencedaily reports on, and there is a reason those experiments are not published in reputable scientific journals