So, what happens when you get a bunch of polyamorous geeks together at a party? Someone starts charting relationship configurations, and someone else starts wondering how many possible relationship configurations there are in a particular group, and someone else gets out a calculator and a sheet of paper, and…
As it turns out, the equation that will tell you for any size group of people n how many possible relationship configurations (couples, triads, and so on) are possible within that group is pretty complicated. It took a lot of work and many sheets of paper, and the considerable brainpower of a couple people with degrees in mathematics, but the equation is:
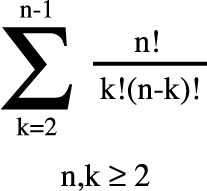
This will tell you for any group of people n how many possible relationship configurations exist in that group.
And the number goes up fast. Scary fast. For n=9, there are 502 possible relationship configurations in that group. The number of people in the Squiggle I belong to is 15; I haven’t calculated the number of possible relationship configurations exist in such a group.
I think I’m going to make this formula into a T-shirt.
Jeez Franklin, quit being a geek & get back to the party :-p
Jeez Franklin, quit being a geek & get back to the party :-p
6,355 (assuming I didn’t screw anything up).
6,355 (assuming I didn’t screw anything up).
That’s a standard combinational formala for “n choose r”
eg
http://www.mathsrevision.net/alevel/pure/binomial.php
That was a formula taught to me at age 16 or 17; before I went to university. Ouch, over 2 decades ago. The mathematicians in your group should have known it without thinking!
ep. Actually, early on in the conversation, one of the math geeks said something along the line of “This looks a lot like Pascal’s Triangle” to me, and predicted that the final equation would be a Riemann sum of “n choose r.” He turned out to be right, of course, but we had to do a lot of arguing and scribbling on sheets of paper before we believed him. 🙂
That’s a standard combinational formala for “n choose r”
eg
http://www.mathsrevision.net/alevel/pure/binomial.php
That was a formula taught to me at age 16 or 17; before I went to university. Ouch, over 2 decades ago. The mathematicians in your group should have known it without thinking!
josh (who understood this equation and has your same “got DSS?” shirt) wants to know what k is.
I’m thinking k is just a counter, and n is the number of people in the group.
Bingo. n is the size of the group; k is the counter for the Riemann sum.
josh (who understood this equation and has your same “got DSS?” shirt) wants to know what k is.
Oh, good gracious. That’s kinda frightening. I’ll have to show that one to my computer-scientist husband…
Oh, good gracious. That’s kinda frightening. I’ll have to show that one to my computer-scientist husband…
I’m thinking k is just a counter, and n is the number of people in the group.
Wait a sec… I don’t think this formula will work for a group of three… you’d end up with a zero in the denominator, wouldn’t you?
Nope, because you’d only have one term to sum: 3!/(2!1!) which is 6/(2*1) = 3. His formula doesn’t count the everyone-relationship, singleton relationships (it takes at least two to tango in Tacit’s world) or the trivial nil relationship.
The sum shouldn’t have excluded the everyone-relationship (that means the original version of the formula was off by one), but does intentionally exclude singletons and the nil relationship.
Wait a sec… I don’t think this formula will work for a group of three… you’d end up with a zero in the denominator, wouldn’t you?
Nope, because you’d only have one term to sum: 3!/(2!1!) which is 6/(2*1) = 3. His formula doesn’t count the everyone-relationship, singleton relationships (it takes at least two to tango in Tacit’s world) or the trivial nil relationship.
You do realise that n!/(k!(n-k)!) are just entries in the nth row of Pascal’s Triangle, and that the sum of any row in Pascal’s Triangle is 2^n right? Take away the k=0, k=1, and k=n entries (which are 1, n, and 1 respectively) and you get as a closed form 2^n-n-2.
I get, by both closed form and summing the damn thing, 501 for n=9 instead of your 502, and I get 32768-15-2 = 32751 for n=15.
Of course, I recognised Pascal’s Triangle instantly.
Actually, that brings up a good point; the Riemann sum given here doesn’t consider the n-case (that is, there should be 4 possibilities in a triad, the three dyads plus the triad itself). There are 502 possibilities for n=9, if you count the 9-some case as well. Didn’t catch that last night; we need to add one to the result.
We (well, not me, but the math geeks among us) recognized the solution once we closed in on it, but we took a very backward and circuitous route to get there.
You do realise that n!/(k!(n-k)!) are just entries in the nth row of Pascal’s Triangle, and that the sum of any row in Pascal’s Triangle is 2^n right? Take away the k=0, k=1, and k=n entries (which are 1, n, and 1 respectively) and you get as a closed form 2^n-n-2.
I get, by both closed form and summing the damn thing, 501 for n=9 instead of your 502, and I get 32768-15-2 = 32751 for n=15.
Of course, I recognised Pascal’s Triangle instantly.
ep. Actually, early on in the conversation, one of the math geeks said something along the line of “This looks a lot like Pascal’s Triangle” to me, and predicted that the final equation would be a Riemann sum of “n choose r.” He turned out to be right, of course, but we had to do a lot of arguing and scribbling on sheets of paper before we believed him. 🙂
Bingo. n is the size of the group; k is the counter for the Riemann sum.
Actually, that brings up a good point; the Riemann sum given here doesn’t consider the n-case (that is, there should be 4 possibilities in a triad, the three dyads plus the triad itself). There are 502 possibilities for n=9, if you count the 9-some case as well. Didn’t catch that last night; we need to add one to the result.
We (well, not me, but the math geeks among us) recognized the solution once we closed in on it, but we took a very backward and circuitous route to get there.
The sum shouldn’t have excluded the everyone-relationship (that means the original version of the formula was off by one), but does intentionally exclude singletons and the nil relationship.
When I was taking Discrete Math, using k as a variable bugged the shit out of me because my science classes had conditioned me to think of k as a constant.
In this case, though the denominator almst spells out “kink!”, which I think outweighs it.
When I was taking Discrete Math, using k as a variable bugged the shit out of me because my science classes had conditioned me to think of k as a constant.
In this case, though the denominator almst spells out “kink!”, which I think outweighs it.